선형대수학을 하다보면 이런저런 학창시절에 배운 수학 지식이 필요하다. 학창시절에 수학을 하고, 성인 되고나서는 거의 안하다 시피 해서 까먹었는데 요즘 인공지능을 공부하다 보니 다시 선형대수학을 공부하며 나머지 수학 지식들도 정리중이다. 공부하다보니, 시간이 촉박하여 잘 정리하지는 못하는데 수학적인 지식을 오랜만에 정리해보려고 한다.
벡터의 내적
벡터의 내적(inner product) 를 이해하기 위해서는 여러가지 수학적 지식을 필요로 한다. 이 글을 읽는 독자들은 나만큼 수학에 무지하다는 생각으로 글을 작성하겠다. 일단, 벡터의 내적을 이해하기 위해서는 삼각함수의 지식을 필요로 한다. 삼각함수 부터 들어가보자.
삼각함수
삼각함수는 쉽게 말해 각(theta) 를 기준으로 인접한 변사이의 비율을 나타내는 것이다. 예를 들면, 아래 그림에서 삼각비는 어떻게 전개 될까?

$$ \cos \theta = 3/5, \sin \theta = 4/5, \tan \theta = 4/3$$
위와 같이 식이 전개됨을 확인할 수 있다.
정사영(Projection)
정사영은한 벡터를 다른 벡터의 방향으로 그림자를 내리는 과정이다. 수직선을 그어 투영된 부분을 찾고, 그 길이와 방향을 벡터로 나타낸 것이 정사영 벡터이다. 쉽게 말하면 해당 벡터의 방향으로 90도인 선분(직교하도록)을 그은 뒤 같은 방향으로 벡터를 하나 그려줬다고 생각하면 된다. 조금 쉽게 이야기 하면, 위의 그림의 a 선분에서 b 선분을 향해 90도인 선을 하나 그리면 된다. 즉, 아래 그림과 같이 될것이다.

눈치가 빠른 사람은 그림만 봐도 알수 있겠지만 정사영(Projection) 시킨것은 사실 아래식과 같음을 알 수 있다.
$$\text{proj}_\mathbf{b} \mathbf{a} = \|\mathbf{a}\| * \cos \theta $$
위의 그림은 살짝 보기 힘드니 vector b 를 조금 더 앞으로 가도록 스케일업 해보도록 하자.
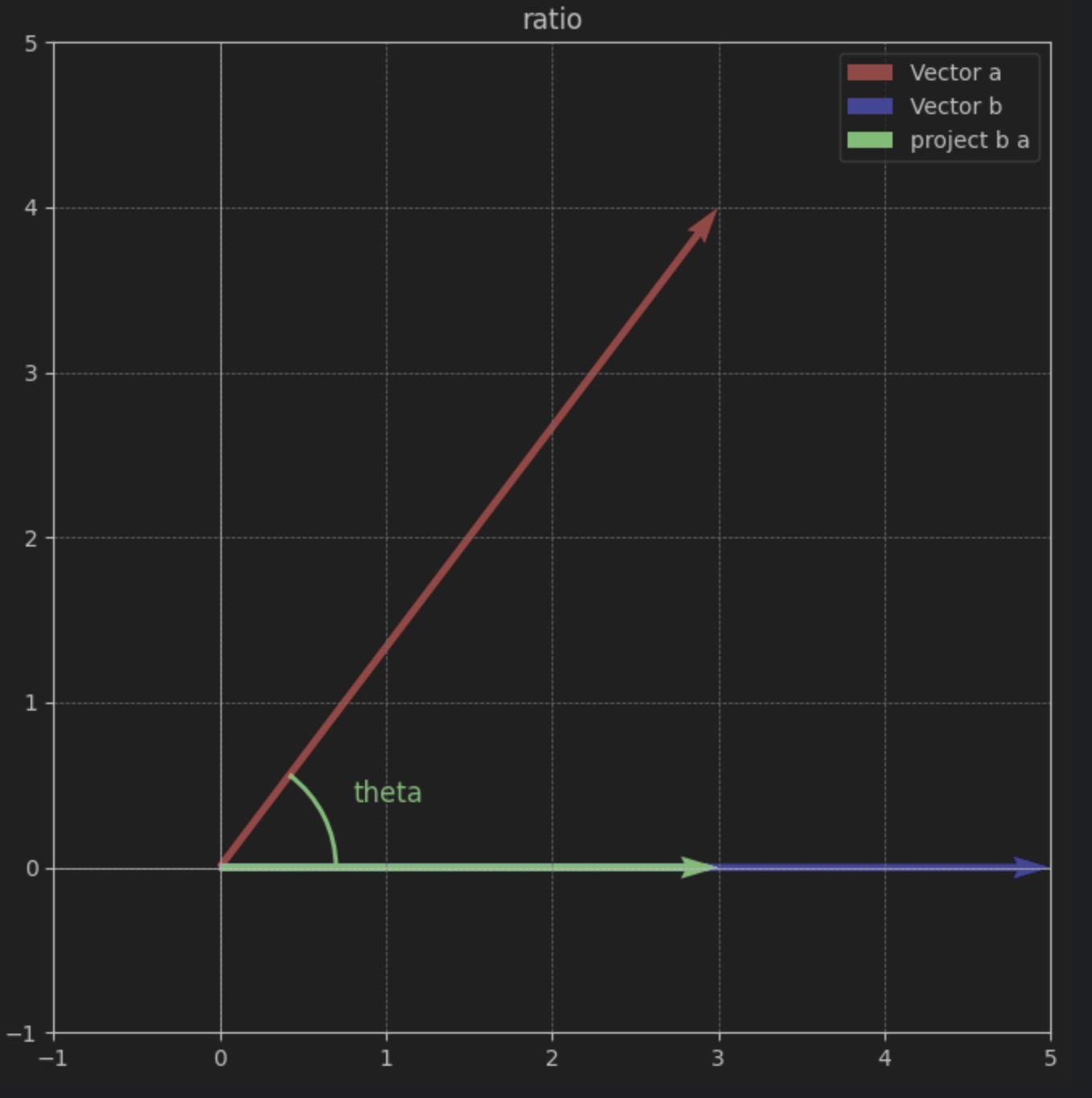
위와 같이 스케일 업을 해보면 vector a 를 vector b 로 정사영시키면 조금 더 짧은 길이 이지만 같은 방향을 지닌 벡터를 얻었음을 알 수 있다. 벡터는 방향성을 지니기 때문에 이러한 정사영(Projection) 이라는 개념이 조금 중요시 되는데, 쉽게 이야기하면 vector b 로 우리는 물체를 (0, 0) 에서 보내려 했을때 vector a 방향으로 힘을 주게 되면 얼마만큼 효율적일까? 를 계산하기 위해 정사영의 개념을 사용한다.
벡터의 내적
이 개념이 중요한 이유는 내적을 알기 위해 중요한 이유를 내적 식과 함께 알아보도록 하자.
$$ {a} \cdot {b} = \|{a}\| * \|{b}\| * \cos \theta $$
위의 수식을 조금만 알기 쉽게 우리가 이전에 봤던 식이랑 비슷하게 순서만 바꿔보자.
$$ \mathbf{a} \cdot \mathbf{b} = \|\mathbf{a}\| \cos \theta \|\mathbf{b}\| $$
식을 위와 같이 순서를 바꿔보면 아래와 같이 아까의 정사영식이 보인다. 만약 우리가 정사영된 벡터의 길이를 구한다면 어떻게 나올까? 일단 정사영된 벡터를 구하는 공식을 알아보자.
$$ \text {proj}_\mathbf{b} \mathbf{a} = \frac{\mathbf{a} \cdot \mathbf{b}}{\mathbf{b} \cdot \mathbf{b}} \cdot \mathbf{b} $$
정사영된 벡터의 길이를 구하는 건 여기서 정사영의 길이를 구해보자
$$ \|\text {proj}_\mathbf{b} \mathbf{a} \| = |\frac{\mathbf{a} \cdot \mathbf{b}}{\mathbf{b} \cdot \mathbf{b}}| \cdot \|\mathbf{b}\| $$
$$ \|\text {proj}_\mathbf{b} \mathbf{a} \| = |\frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{b}^2\|}| \cdot \|\mathbf{b}\| $$
$$ \|\text {proj}_\mathbf{b} \mathbf{a} \| = \frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{b}\|} $$
즉, 이렇게 놓고 보면 정사영된 길이에 벡터 b 의 크기를 곱하면 결국 해당 벡터의 사이즈를 얻을 수 있음을 역순으로 알 수 있다.
'Math' 카테고리의 다른 글
| Calculas) Limit (0) | 2025.03.31 |
|---|---|
| Calculas 1 (0) | 2025.03.31 |
| Inclusion / Exclusion Of Elements (0) | 2022.06.20 |
| Algebraic Properties And Equations (0) | 2022.06.19 |